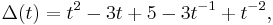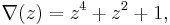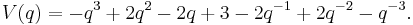6₃ knot

In knot theory, the 6₃ knot is one of three prime knots with crossing number six, the others being the stevedore knot and the 6₂ knot.

Like the figure-eight knot, the 6₃ knot is amphichiral, meaning that it is indistinguishable from its own mirror image. It is also invertible, meaning that orienting the curve in either direction yields the same oriented knot.

The Alexander polynomial of the 6₃ knot is

$\Delta(t) = t^2 - 3t %2B 5 - 3t^{-1} %2B t^{-2}, \,$

the Conway polynomial is

$\nabla(z) = z^4 %2B z^2 %2B 1, \,$

and the Jones polynomial is

$V(q) = -q^3 %2B 2q^2 - 2q %2B 3 - 2q^{-1} %2B 2q^{-2} - q^{-3}. \,$ ^[1]

The 6₃ knot is a hyperbolic knot, with its complement having a volume of approximately 5.69302.

References

^ 6 3 - Knot Atlas